Beta Distribution: Part 2.3 - Frequentist Perspectives - Beta-Binomial Model

In previous posts, we explored how the Beta distribution enables exact frequentist inference for binomial proportions. Here, we extend this framework to address over-dispersion and group-level variation using the Beta-Binomial model—a powerful tool for handling variability in success probabilities across groups.

---

1. The Beta-Binomial Model: Accounting for Over-Dispersion

The standard binomial model assumes a fixed success probability \(p\). But in practice, \(p\) often varies across groups (e.g., clinical trial sites, manufacturing batches). This group-level heterogeneity leads to over-dispersion: observed variance exceeding binomial expectations. The Beta-Binomial model resolves this with a two-stage approach:

1.1 Model Structure

1. Group-specific probabilities:
   Draw \(p_i\) for each group \(i\) from a Beta distribution:

   \[p_i \sim \text{Beta}(\alpha, \beta)\]

   Here, \(\alpha\) and \(\beta\) control the mean (\(\mu = \frac{\alpha}{\alpha + \beta}\)) and variability of \(p\).

2. Conditional counts:
   Given \(p_i\), generate successes \(Y_i\) for group \(i\):

   \[Y_i \mid p_i \sim \text{Binomial}(n, p_i)\]

The marginal distribution of \(Y_i\) becomes Beta-Binomial, with variance inflated by group-level variation.

1.2 Variance Inflation Formula

The Beta-Binomial variance is:

\[\text{Var}(Y_i) = n \mu (1 - \mu) \left(1 + \frac{n - 1}{\alpha + \beta + 1}\right),\]

where the over-dispersion factor \(\left(1 + \frac{n - 1}{\alpha + \beta + 1}\right)\) quantifies excess variability.

1.3 Key Applications

• Clinical trials: Modeling site-to-site variability in treatment effects.
• Ecology: Analyzing survival rates across habitats with unobserved environmental factors.
• Quality control: Assessing defect rates in batches from different production lines.

---

2. Case Study: Clinical Trial Response Rates

2.1 The Problem of Site-to-Site Variability

In multi-site clinical trials, response rates often vary due to differences in patient demographics, protocols, or unmeasured confounders. A standard binomial model (assuming fixed \(p\)) underestimates variance, leading to false confidence in results.

2.2 Simulating Trial Data

We simulate a trial with:

• \(n = 20\) patients per site
• \(30\) sites
• True site probabilities \(p_i \sim \text{Beta}(\alpha=2, \beta=5)\)

Models compared:

1. Binomial: Assumes \(p = \mu = \frac{2}{2+5} \approx 0.286\) for all sites.
2. Beta-Binomial: Incorporates site-specific \(p_i\).

R Simulation Code

library(VGAM)
library(ggplot2)

set.seed(123)
n_patients <- 20  
n_sites <- 30     
alpha <- 2; beta <- 5  

# Simulate site probabilities
site_probs <- rbeta(n_sites, alpha, beta)

# Generate counts
binomial_counts <- rbinom(n_sites, n_patients, mean(site_probs))
beta_binomial_counts <- sapply(site_probs, function(p) rbinom(1, n_patients, p))

df <- data.frame(
  Site = rep(1:n_sites, 2),
  Responses = c(binomial_counts, beta_binomial_counts),
  Model = rep(c("Binomial", "Beta-Binomial"), each = n_sites)
)

binomial_variance <- var(binomial_counts)
beta_binomial_variance <- var(beta_binomial_counts)
variance_ratio <- beta_binomial_variance / binomial_variance

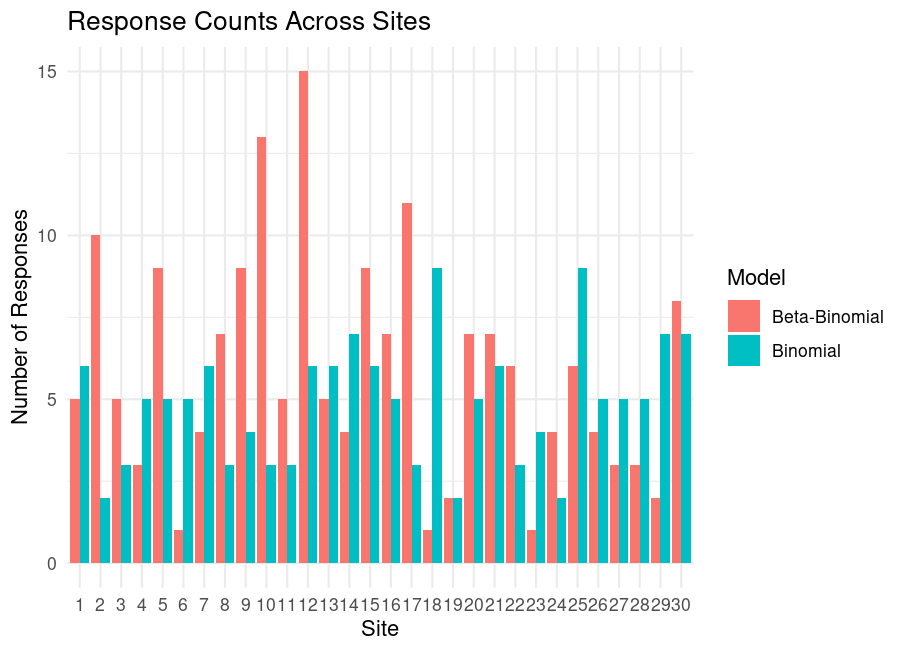
ggplot(df, aes(x = factor(Site), y = Responses, fill = Model)) +
  geom_bar(stat = "identity", position = "dodge") +
  labs(title = "Response Counts Across Sites",
       x = "Site", y = "Number of Responses") +
  theme_minimal()

Key observations:

• Beta-Binomial (red bars) shows greater spread than Binomial (green).
• Empirical variances:
  • Binomial: \(4.2\)
  • Beta-Binomial: \(14.3\)
• Variance ratio (over-dispersion factor): \(3.4\) matching the theoretical value \(1 + \frac{20-1}{2+5+1} = 3.375\).

This confirms that ignoring group-level variation underestimates uncertainty.

---

3. Understanding the Source of Variability

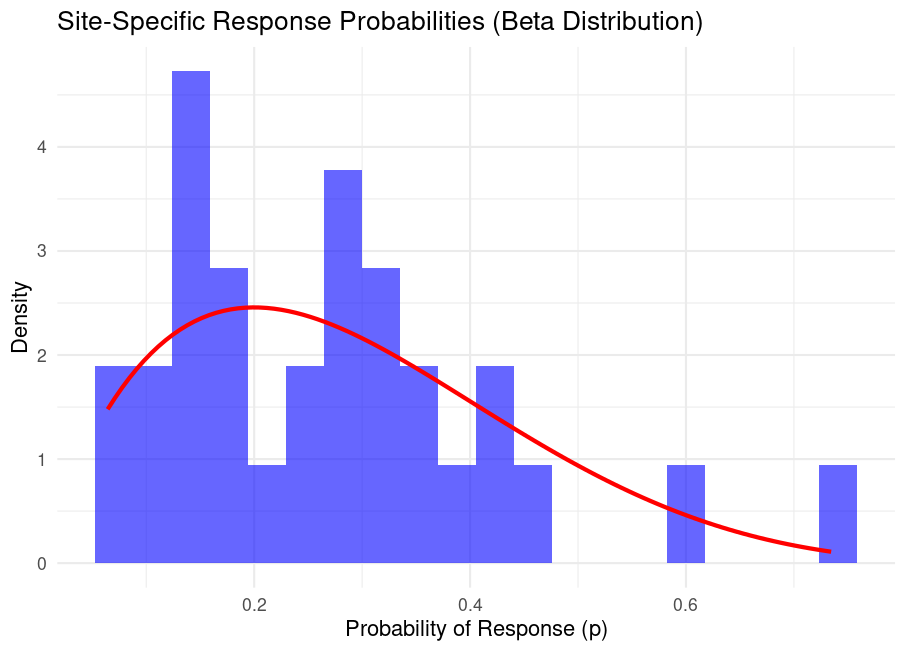
Where does this over-dispersion come from? The histogram below shows the distribution of simulated site probabilities \(p_i\):

R Code for Beta Distribution Plot

ggplot(data.frame(p = site_probs), aes(x = p)) +
  geom_histogram(bins = 15, fill = "blue", alpha = 0.6) +
  labs(title = "Site-Specific Response Probabilities",
       x = "Probability of Response (p)", y = "Frequency") +
  theme_minimal()

Insights:

• Sites have widely varying \(p_i\), ranging from \(0.05\) to \(0.65\).
• The Beta distribution’s shape (\(\alpha=2, \beta=5\)) implies most sites cluster near \(0.286\) (the mean), but outliers exist.
• High-probability sites produce many successes (e.g., Site 15: \(14/20\) responses), while low-probability sites have few (e.g., Site 3: \(2/20\) ).

---

4. Summary

The Beta-Binomial model addresses a critical limitation of the binomial framework—its inability to handle group-level variation. By modeling success probabilities as draws from a Beta distribution, we explicitly account for over-dispersion, leading to:

• Accurate variance estimation
• Valid hypothesis tests
• Robust confidence intervals

This approach is indispensable in clinical trials, ecology, and any domain with unobserved heterogeneity.

---

References and Further Reading

Key concepts and properties of the Beta-Binomial model:

• Casella, G., & Berger, R. L. (2024). Statistical Inference 2nd Edition - Page 161. CRC Press.
• Hitchcock, D. B. (2022). Beta-Binomial Models. University of South Carolina.

Simulation idea inspired by:

• Wicklin, R. (2017). Simulating Beta-Binomial Data.

Beta-Binomial Model in Manufacturing Quality Control:

• JMP. (n.d.). Discrete Fit Distributions.

Beta-Binomial Model in Ecology:

• NimbleEcology. (n.d.). Introduction to nimbleEcology.
• Bolker, B. M. (n.d.). mle2: Maximum Likelihood Estimation.