Reinformant Learning: Tabular Q-Learning Implementation and Debugging

Introduction

Reinforcement Learning (RL) is a fascinating area of machine learning where an agent learns to make decisions by interacting with an environment. One of the foundational algorithms in RL is Q-learning, specifically Tabular Q-learning. This article aims to delve into the theory, principles, and mathematics behind Tabular Q-learning, followed by a detailed walkthrough of my implementation. I will also share my debugging process, illustrating how the results evolved through each step, and provide an analysis of the outcomes.

Theory and Principles of Tabular Q-Learning

The Reinforcement Learning Framework

In RL, an agent interacts with an environment over discrete time steps. At each time step \(t\), the agent:

1. Observes the current state \(s_t\).
2. Chooses an action \(a_t\) based on a policy \(\pi\).
3. Receives a reward \(r_{t+1}\) and transitions to a new state \(s_{t+1}\).

The goal of the agent is to learn a policy \(\pi\) that maximizes the cumulative reward over time.

Q-Learning

Q-learning is an off-policy RL algorithm that aims to learn the optimal action-value function \(Q^*(s, a)\), which represents the maximum expected cumulative reward achievable from state \(s\) by taking action \(a\) and following the optimal policy thereafter.

The Q-value update rule is given by:

\[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \right]\]

where:

• \(\alpha\) is the learning rate.
• \(\gamma\) is the discount factor.
• \(r_{t+1}\) is the reward received after taking action \(a_t\) in state \(s_t\).
• \(\max_{a'} Q(s_{t+1}, a')\) is the maximum Q-value for the next state \(s_{t+1}\).

Tabular Q-Learning

In Tabular Q-learning, the Q-values are stored in a table (or matrix) \(Q[s, a]\). This approach is feasible for environments with a small, discrete state and action space.

Epsilon-Greedy Policy

The epsilon-greedy policy is a strategy used to determine the actions an agent should take given its current state. In RL, the agent needs to explore the environment to discover the optimal policy. If the agent only exploits its current knowledge (exploitation: always choosing the action with the highest Q-value), it may get stuck in a local optimum and miss out on better long-term strategies. On the other hand, if the agent takes actions completely at random (exploration), it may never learn the best actions to take, leading to poor performance.

Epsilon-greedy balances exploration and exploitation by selecting a random action with probability \(\epsilon\) (exploration) and the action with the highest Q-value with probability \(1 - \epsilon\) (exploitation). It ensures that the agent explores the environment sufficiently while still exploiting known good actions to maximize rewards.

Formally, the action selection can be described as:

\[a_t = \begin{cases} \text{random action} & \text{with probability } \epsilon \\ \arg\max_a Q(s_t, a) & \text{with probability } 1 - \epsilon \end{cases}\]

Implementation and Debugging

Environment Setup

For this implementation, I used the classic Gridworld environment. The agent starts at a random position and aims to reach a goal position while avoiding obstacles.

Q-Learning Algorithm

My initial implementation of the Tabular Q-learning algorithm in Python is as follows (Code Version 0):

# Code Version 0
def epsilon_greedy(state, Q, epsilon):
    if random.uniform(0, 1) < epsilon:
        return random.randint(0, action_space_size - 1)  # Explore
    else:
        return np.argmax(Q[state, :])  # Exploit

def tabular_q_learning(Q, state, action, reward, next_state, terminal): if not terminal:
    q[state, action] = 0
    if not terminal:
      max_q_value_next_state = 0
    else:
      max_q_value_next_state = np.max(Q[next_state, :])
      Q[state, action] = (1 - alpha) * Q[state, action] + alpha * (reward + gamma * max_q_value_next_state)

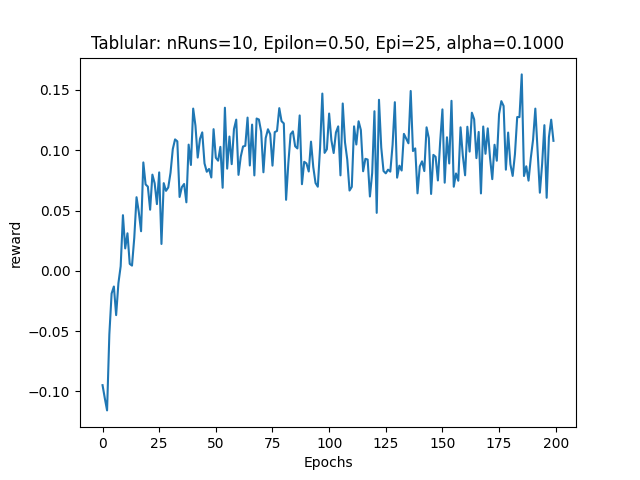
When I ran the code, I encountered a bug where the Q-values were not updating correctly, leading to suboptimal learning performance as shown in the graph below:

The cumulative rewards were near 0 (Avg Revard = 0.09), indicating that the agent was not learning. I quickly realized that the issue was due to the Q-value update logic, in which I initiate the Q-value as 0 for each iteration. I removed the line q[state, action] = 0 and reran the code (Code Version 1).

# Code Version 1
def tabular_q_learning(Q, state, action, reward, next_state, terminal): if not terminal:
    if not terminal:
      max_q_value_next_state = 0
    else:
      max_q_value_next_state = np.max(Q[next_state, :])
      Q[state, action] = (1 - alpha) * Q[state, action] + alpha * (reward + gamma * max_q_value_next_state)

The cumulative rewards improved slightly, but the learning performance was still suboptimal (Avg Reward = 0.23):

Looking at the code, I realized that the Q-value is not correctly updated. It should be updated regardless of whether the state is terminal or not. I modified the code as following (Code Version 2):

# Code Version 2
def tabular_q_learning(Q, state, action, reward, next_state, terminal): if not terminal:
    if not terminal:
      max_q_value_next_state = 0
    else:
      max_q_value_next_state = np.max(Q[next_state, :])
    Q[state, action] = (1 - alpha) * Q[state, action] + alpha * (reward + gamma * max_q_value_next_state)

The cumulative rewards again improved significantly (Avg Reward = 0.36), but still not optimal: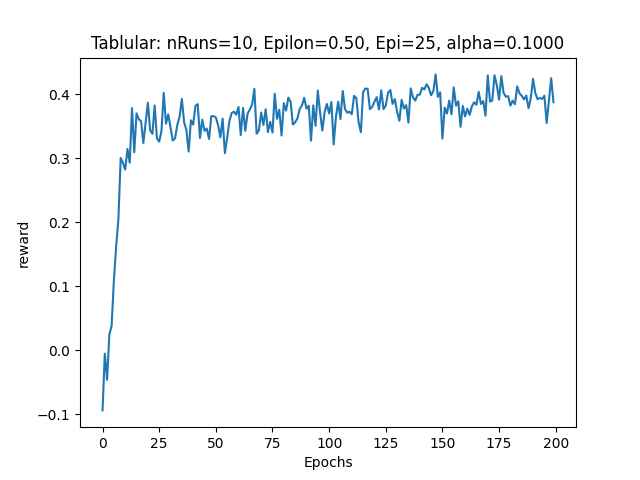

I finally realized that the issue was due to the incorrect handling of the terminal state. I updated the code to correctly set the maximum Q-value for the next state as 0 in the terminal state. The corrected code is as follows (Code Version 3):

# Code Version 3
def tabular_q_learning(Q, state, action, reward, next_state, terminal): if not terminal:
    if terminal:
      max_q_value_next_state = 0
    else:
      max_q_value_next_state = np.max(Q[next_state, :])
    Q[state, action] = (1 - alpha) * Q[state, action] + alpha * (reward + gamma * max_q_value_next_state)

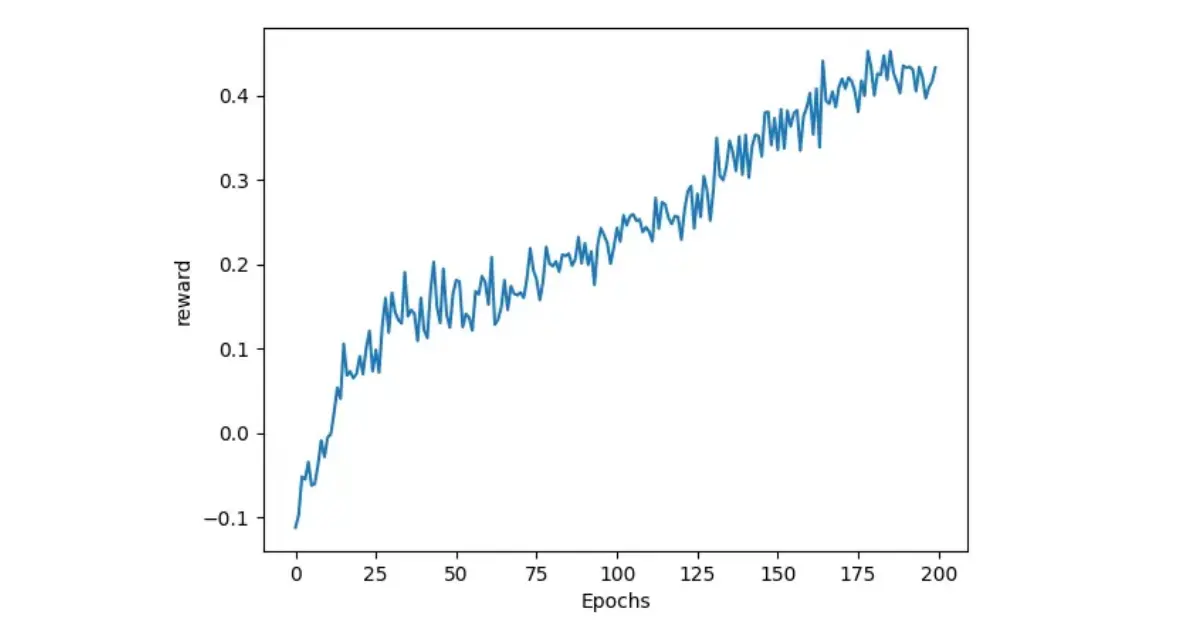
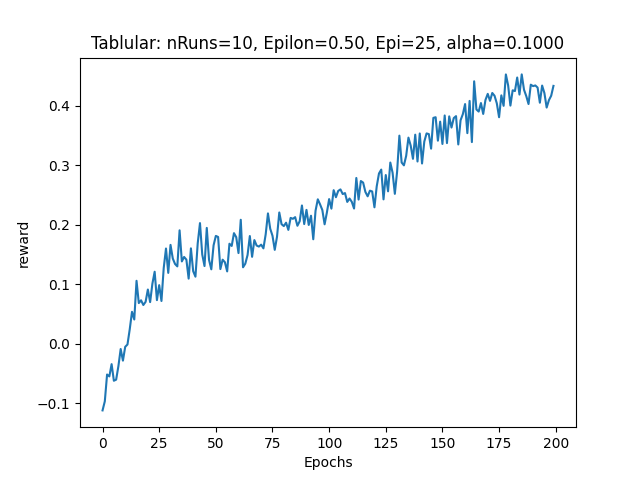
The output of the corrected code showed higher cumulative rewards (Avg Rewards = 0.5) as shown in the graph below: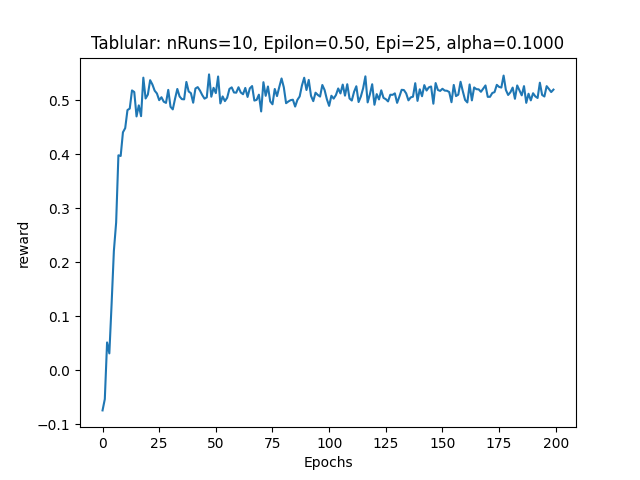

Analysis

Let’s analyze each version of the wrong and correct code to see why the results evolved as they did.

For Code Version 0, the Q-value is initialized as 0 for each iteration, and the update only happnes at within the else clause which corressponds to the terminal state. This leads to the Q-value not being updated all, resulting in almost 0 cumulative rewards (Avg Reward = 0.09).

For Code Version 1, the Q-value initialization was removed, but the update logic was still incorrect. The Q-value update only occurred in the else clause, which corresponded to the terminal state. This resulted in suboptimal learning performance (Avg Reward = 0.23).

For Code Version 2, the Q-value update logic was corrected, but the handling of the terminal state was still incorrect. The Q-value got updated in every state, but the max Q-value for the next state \(\max_{a'} Q(s_{t+1}, a')\) only calcualted when the state is terminal otherwise it is set to 0. Thus in each iteration before the terminal state we wrongly update the Q-value as:

\[Q(s_t, a_t) = (1 - \alpha) \cdot Q(s_t, a_t) + \alpha \cdot (r_{t+1} + \gamma \cdot 0)\]

This explains why the agent’s learning performance was still suboptimal. However since this version updates the Q-value in every state, the cumulative rewards improved compared to version 2 (Avg Reward = 0.36 > 0.23).

Finally, in Code Version 3, the terminal state handling was corrected, and the Q-value update logic was fixed. This resulted in the agent learning more effectively and achieving higher cumulative rewards (Avg Reward = 0.5).

Terminal State Handling

In the terminal state, there are no future rewards to be gained, so the maximum Q-value for the next state is set to 0. This ensures that the Q-value update only considers the immediate reward. Below are some senarios of wrong setup at terminal state and the retional:

• If we did a normal update, it would incorrectly factor in future rewards that do not exist.
• Setting the whole Q-table to 0 at terminal state would erase all learned information, which is undesirable.
• If we pass the terminal state, the Q-value would not be updated at terminal state. This is wrong because the immediate reward at the terminal state often signifies the achievement of a goal. Thus we should not ignore the immediate reward at the terminal state, even there is no future states or rewards.

Conclusion

By implementing and debugging Tabular Q-learning, I gained a deeper understanding of the algorithm and the importance of correct implementation details. The process of identifying and rectifying bugs helped me appreciate the nuances of RL algorithms and the impact of small errors on learning performance.